2. 河北大学公共卫生学院,河北 保定 071000
2. School of Public Health, Hebei University, Baoding 071000, China
肺结核是一种由结核分枝杆菌感染引起的、经呼吸道传播的慢性传染病,其传染性强,若不加干预,1例阳性患者年平均可感染10~15名易感者[1],若发生规模性疫情则会对社会造成重大影响。2021年中国报告肺结核639 548例,死亡1 763人,报告发病率为45.365 1/10万,报告死亡率为0.125 1/10万,在乙类传染病中发病数和死亡数排第2位。近年来,在肺结核发病的流行状况研究中,趋势预测分析成为国内学者的关注点。研究[2-3]使用差分自回归移动平均模型(ARIMA)及其拓展模型进行肺结核发病数短期预测;还有学者使用灰色系统GM(1, 1)模型、指数平滑法和Joinpoint回归模型等分析肺结核发病数趋势[4-6]。已有的方法模型在局部区域各自取得了较好的应用效果,但在全国范围还未得到实证。考虑到肺结核发病具有显著周期性和季节性[7],为提高预测精度,本文借鉴刘超等[8]对呼吸道传染病的研究方法,采用CensusX-13季节调整法研究肺结核的季节性特征和循环周期特征,以掌握中国肺结核流行趋势,作出长短期预测,为中国肺结核的预警防控提供参考。
1 资料与方法 1.1 资料选取2010年1月—2021年12月中国疾病预防控制局法定传染病报告中国内肺结核发病的月度数据。中国疾病预防控制局法定传染病报告包含多种甲、乙、丙类传染病发病及死亡的月度、年度数据。
1.2 方法 1.2.1 CensusX-13季节调整法根据CensusX-13季节调整法,肺结核时间序列由趋势循环因素、季节因素和不规则因素3部分组成。通过将各因素分解可以更加直观地观察到肺结核报告发病的季节特征和趋势循环特征,以趋势循环因素反映我国肺结核报告发病数的长期规律。根据“波峰~波峰”的周期划分循环周期[9]。
| $ T = {T_{tc}} + {T_s} + {T_i} $ | (1) |
其中,T代表肺结核报告发病数,Ttc为趋势循环因素,Ts为季节因素,Ti为不规则因素。
1.2.2 Hodrick-Prescott(HP)滤波法根据HP滤波法,肺结核报告发病趋势循环因素可分解为长期趋势因素和循环周期因素两部分,由此提取我国肺结核报告发病周期。
| $ {T_{tc}} = {T_t} + {T_c} $ | (2) |
其中,Tt代表肺结核报告发病的长期趋势因素,反映研究期间肺结核报告发病数的趋势变化;Tc为循环周期因素。采用HP滤波法从趋势循环因素中分离出长期趋势因素,得到数据的循环周期因素,反映我国肺结核报告发病数以一定时间间隔起伏波动的规律,从而判断一段时间内肺结核报告发病包含几个循环周期,探讨每个循环周期的长度和波动幅度。
1.2.3 线性回归模型长期趋势因素呈现出明显的线性特征,对长期趋势作线性回归,基于此对我国肺结核报告发病数作出长期预测。线性回归可表示为:
| $ {T_t} = {\beta _1}x + {\beta _2} + \mu $ | (3) |
其中,自变量x为时间,β1和β2分别为回归系数和常数项,μ为随机误差。
1.2.4 Holt-Winter季节指数平滑模型Holt-Winter季节指数平滑模型是在Holt模型的基础上引入Winter季节因素,对我国肺结核报告发病数进行短期预测,可表示为:
| $ {H_t} = \alpha \frac{{{D_t}}}{{{S_{t - l}}}} + (1 - \alpha )\left( {{H_{t - 1}} + {D_{t - 1}}} \right) $ | (4) |
| $ {L_t} = \beta \left( {{H_t} - {H_{t - 1}}} \right) + (1 - \beta ){L_{t - 1}} $ | (5) |
| $ {S_t} = \gamma \frac{{{D_t}}}{{{H_t}}} + (1 - \gamma ){S_{t - l}} $ | (6) |
其中,α、β、γ为模型的平滑参数,Ht为稳定性,Lt为趋势性,St为季节性,l为季节周期长度,Dt为t时刻的实际值。
Holt-Winter季节指数平滑模型的预测模型:
| $ {Y_{t + a}} = \left( {{H_t} + a{L_t}} \right){S_{t - l + a}} $ | (7) |
其中,Yt+a为t+a时刻的肺结核报告发病数,a为预测时间与当前时间的时间间隔数。
1.3 统计学分析应用Excel软件对数据进行汇总整理,Eviews软件对数据进行建模,分析肺结核的季节特征、循环周期特征,以及长短期预测。
2 结果 2.1 肺结核发病季节分解根据中国2010年1月—2021年12月肺结核报告发病数的月度数据,绘出时间序列图,并采用CensusX-13季节调整法进行调整,得到剔除季节性的时间序列。可以看出,肺结核报告发病具有明显的季节性特征。每个年度肺结核报告发病数都呈现先下降后上升再下降的变化,报告发病高峰期为3—6月。总体来看,2010—2021年中国肺结核报告发病数呈现逐年下降趋势。从季节调整后的时间序列曲线可以看出,2012年2月和2017年2月分别出现了肺结核报告发病数季节调整后的最高峰和次高峰,2020年2月出现肺结核报告发病数季节调整后的低谷。肺结核报告发病数总体呈下降趋势,短时间内波动明显。见图 1。
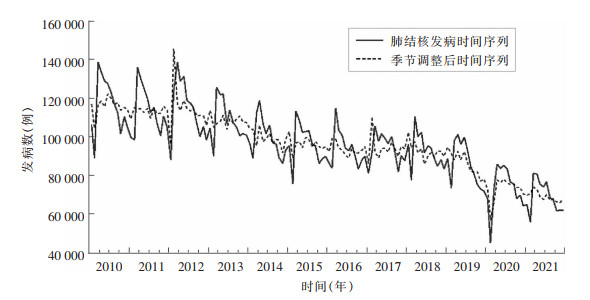 |
| 图 1 2010—2021年中国肺结核病发病时间序列和季节调整后时间序列图 Figure 1 Time series and seasonally adjusted time series of PTB occurrence in China, 2010-2021 |
为分析中国肺结核发病的季节性特征,根据CensusX-13季节调整法,分解出肺结核季节因素的时间序列图,见图 2。我国肺结核发病具有明显的季节性特征:每年有两个高峰期,3—7月为肺结核报告发病高峰期,其中,3月肺结核报告发病数最多,肺结核报告发病数集中在第二季,随后报告发病数下降,到10月出现低谷后有较缓回升的高峰直至春节前,表现为每年2月为报告发病数的最低谷。
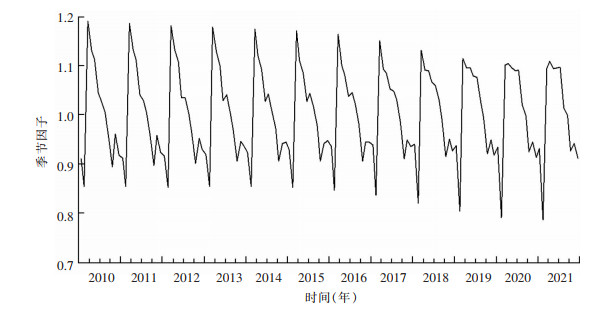 |
| 图 2 2010—2021年中国肺结核病发病的季节性特征 Figure 2 Seasonal characteristics of PTB occurrence in China, 2010-2021 |
根据CensusX-13季节调整法可得到肺结核报告发病的趋势循环因素,进一步使用HP滤波法将肺结核报告发病的趋势循环因素分解为长期趋势因素和循环周期因素。从趋势循环曲线看,除2011年7月—2012年4月报告发病数增长较快外,其他月份都呈现下降趋势。2012年4月—2014年8月及2019年1月—2021年12月这两个时间段,肺结核报告发病数急剧下降。2010年1月—2021年12月中国肺结核报告发病数呈逐年下降的长期趋势。见图 3。
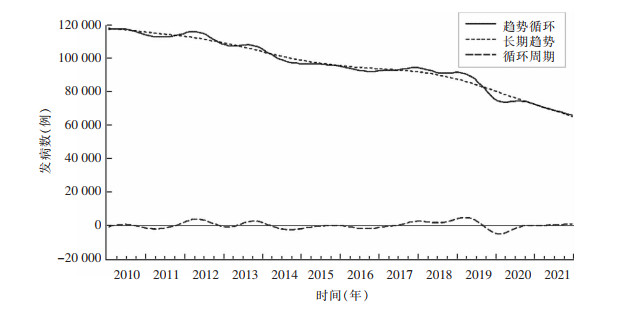 |
| 图 3 2010—2021年中国肺结核病发病的趋势循环、长期趋势和循环周期 Figure 3 Trend cycle, long-term trend and cycle of PTB occurrence in China, 2010-2021 |
循环周期曲线围绕0值上下波动,根据“波峰~波峰”的周期划分,肺结核报告发病大致可分为6个循环周期。肺结核报告发病增高的月份合计为67个月,平均每个周期有11个月发病呈上升趋势。肺结核报告发病降低的月份合计为59个月,平均每个周期有10个月发病呈下降趋势。肺结核循环周期的波动幅度不一,其中波动幅度最大的循环周期为2019年4月—2020年11月,波动幅度最小的循环周期为2018年2月—2019年3月,平均循环周期长度为21个月。见表 1。
| 表 1 2010—2021年中国肺结核发病的循环周期 Table 1 The cycle of PTB occurrence in China, 2010-2021 |
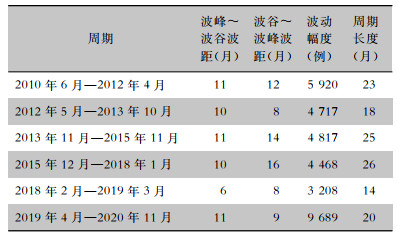
|
通过HP滤波法从趋势循环序列中将长期趋势分离出来,将时间作为自变量,报告发病数作为因变量,并以最小二乘法为原则构建线性回归模型。使用该模型预测年平均趋势值,预测结果见表 2。模型拟合效果较好,相对误差均在7.5%以内,因此使用该模型对肺结核报告发病数进行预测。根据预测结果,2022、2023、2024年肺结核报告发病当年月平均趋势值分别为69 326、65 184、61 042例。
| 表 2 2010—2021年中国肺结核发病每年月平均趋势值 Table 2 Annual average monthly trend of PTB occurrence in China, 2010-2021 |

|
通过使用Holt-Winter季节指数平滑模型对2010年1月—2020年12月中国肺结核每月发病数进行拟合,将拟合后模型的预测结果与2021年发病的月度数据进行对比。结果显示,预测值与实际值的平均相对误差为3.22%,总体预测效果较好。见图 4。
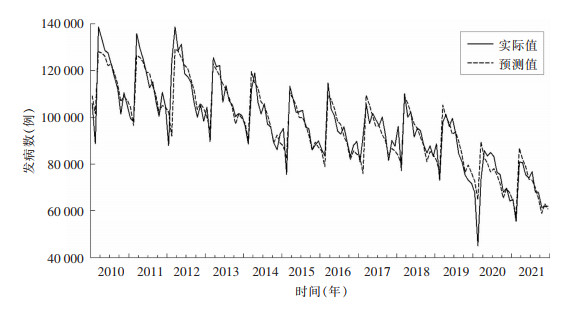 |
| 图 4 2010—2021年中国肺结核病发病实际值与短期预测值对比图 Figure 4 Comparison between the actual value and the short-term prediction value of PTB occurrence in China, 2010-2021 |
近几年,国家为阻断新型冠状病毒感染疫情蔓延采取了一系列防控措施,在一定程度上切断了呼吸道传染病的传播途径,理论上也会减少肺结核发病,降低暴发肺结核疫情的风险。有研究[10-11]指出,疫情明显导致肺结核水平下降。根据2022年8、9月中国甲乙丙类传染病疫情动态概要[12-13],包括肺结核在内的报告发病数居前5位的病种占总发病数的92%及以上,较2021年同期均有上升(8月较同期上升23%),其中,肺结核在乙类传染病报告中发病数居第2位。可见,目前中国肺结核防控依然需要时刻警惕。
过去几十年里,中国作为结核病高负担国家,面临着十分艰巨的卫生挑战,但我国公共卫生事业依然取得了巨大的成就,结核病发病率和病死率不断降低,这是我国积极探索肺结核疾病防治措施,不断开展防控治疗研究,加大防治经费投入,完善监测体系,加强医防合作等各项举措的成果[14-15]。2010—2021年肺结核报告发病数整体呈下降趋势,其中,季节调整后的最高峰为2012年2月,次高峰为2017年2月,究其原因,一是部分因春节假期(1月)延误就诊的患者在假期结束后(2月)就医[16],且延误诊断也会增加肺结核传播风险,使肺结核感染人数增加;二是2012年2月和2017年2月均处于各自循环周期的上升期,气候寒冷,导致2月病例急剧增加。2020年2月出现肺结核报告发病数季节调整后的低谷,可能是突发公共卫生事件对结核病登记情况的短期影响,使报告病例大幅度减少;此外,严格的疫情防控也可以减少肺结核的传播[10-11]。
我国肺结核报告发病具有明显季节性。肺结核报告发病数有两个高峰期,分别为3—7月的“大高峰期”和11月到次年春节前的“小高峰”,低谷有2月“大低谷”和10月“小低谷”。高峰期和低谷期符合我国肺结核流行特征,与既有研究[7]流行期基本一致,与局部区域肺结核流行特征不冲突。其中,春节前后流行高峰期符合冬、春两季发病的季节性特征;肺结核报告发病数集中在第二季度,符合呼吸道疾病传播规律[8];7月全国气候普遍温暖潮湿,有利于肺结核的传播。2月的肺结核报告发病数“大低谷”出现在双高峰之间,是因为2月通常是传统春节所在的月份,容易受到“春节效应”的影响[16]。仅从肺结核报告发病数来看,3—7月肺结核报告发病数量远高于其他时期,3月是该病报告数的最高峰,8—10月肺结核报告发病数下降明显,11月报告发病数上升直至次年春节前。据此,在大、小高峰期来临前应采取预防措施,特别是3—7月,更应加强公共场所的卫生管理,室内勤通风换气,适当体育锻炼提高免疫力,出行佩戴口罩等。
我国肺结核报告发病具有明显的周期性。2010年1月—2021年12月,中国肺结核的发病大致分为6个循环周期,每个不同循环周期内波动幅度不同,波动幅度最大的循环周期为2019年4月—2020年11月,可能与新型冠状病毒感染疫情暴发后采取的一系列措施有关。每个循环周期的长度相近,平均长度为21个月,以最近两个周期为基础推断下一个循环周期为2020年12月—2022年4月,与模型拟合实际数据的结果(2020年12月—2022年3月)基本一致。根据线性回归模型对肺结核发病的长期预测,2022、2023和2024年中国肺结核每年月平均报告发病例数分别为69 326、65 184和61 042,呈下降的长期趋势。短期趋势拟合预测效果较好,说明Holt-Winter季节指数平滑模型可用于对中国肺结核发病进行短期预测。
CensusX-13季节调整法可以较好地处理时间序列数据的季节因素、趋势循环因素及不规则因素,在传染病流行特征研究方面具有较好的应用前景[8],适用于肺结核的季节特征分析,然后采用HP滤波法探究我国肺结核报告发病周期,最后分别采用线性回归模型和Holt-Winter季节指数平滑模型对我国肺结核报告发病进行长短期预测,具有平均相对误差小的特点[17]。本研究在方法模型的分析预测上取得了较好的效果,对于我国肺结核的防控具有一定意义,但受限于肺结核月度数据的可获得性,未能进一步获取审卡后的肺结核报告发病数据,研究结论可能有偏差。
为了更好地控制结核病,有关部门应结合该病的流行特征,在疾病发生高峰前采取有效的预防控制措施。不同地区和人群肺结核发病情况不尽相同。从地区分布来看,新疆和广东是我国肺结核防控的重点区域[18]。从人群分布来看,老人、儿童及免疫力低下人群易感; 男性患肺结核的风险及死亡风险均大于女性[19]; 孕妇因妊娠期掩盖肺结核的症状而导致诊断治疗延迟的风险增高[20]。应对不同地区和人群采取针对性措施,加大对高风险地区和易感人群的保护力度,同时应注意对肺结核患者的心理开导[21], 从而降低结核病的发病率和病死率,减少疾病对患者个人和国家的负担。
利益冲突:所有作者均声明不存在利益冲突。
| [1] |
王翠萍, 郭梦玥, 郎胜利. 2016-2020年内蒙古自治区肺结核患者就诊延迟影响因素分析[J]. 疾病监测, 2023, 38(2): 152-156. Wang CP, Guo MY, Lang SL. Influencing factors of treatment delay in pulmonary tuberculosis patients in Inner Mongolia, 2016-2020[J]. Disease Surveillance, 2023, 38(2): 152-156. |
| [2] |
刘伟, 刘远, 胡文穗, 等. 差分自回归移动平均乘积季节模型预测广州市肺结核发病趋势[J]. 中华疾病控制杂志, 2021, 25(2): 240-243, 248. Liu W, Liu Y, Hu WS, et al. Application of multiple seasonal ARIMA model for predicting the incidence trend of tuberculosis in Guangzhou City[J]. Chinese Journal of Disease Control & Prevention, 2021, 25(2): 240-243, 248. |
| [3] |
付之鸥, 周扬, 陈诚, 等. 时间序列分析与机器学习方法在预测肺结核发病趋势中的应用[J]. 中国卫生统计, 2020, 37(2): 190-195. Fu ZO, Zhou Y, Chen C, et al. Application of time series analysis and machine learning methods in predicting the incidence of tuberculosis[J]. Chinese Journal of Health Statistics, 2020, 37(2): 190-195. |
| [4] |
张芳, 王玉兰, 刘晶磊, 等. 北京市东城区2013-2019年肺结核流行病学特征及疫情趋势预测[J]. 中国预防医学杂志, 2020, 21(8): 918-922. Zhang F, Wang YL, Liu JL, et al. Epidemiological characteria-tics and epidemic trend prediction of pulmonary tuberculosis in Dongcheng district of Beijing in 2013-2019[J]. Chinese Preventive Medicine, 2020, 21(8): 918-922. |
| [5] |
卞子龙, 卓莹莹, 贺志强, 等. 应用乘积季节模型与指数平滑模型预测上海市肺结核疫情[J]. 南京医科大学学报(自然科学版), 2021, 41(2): 268-273. Bian ZL, Zhuo YY, He ZQ, et al. Application of multiple seasonal model and exponential smoothing model in predicitng pulmonary tuberculosis epidemic in Shanghai[J]. Journal of Nanjing Medical University(Natural Sciences), 2021, 41(2): 268-273. |
| [6] |
董智强, 刘伟, 胡文穗, 等. 2006-2020年广州市儿童肺结核流行特征及变化趋势[J]. 中国感染控制杂志, 2021, 20(9): 801-806. Dong ZQ, Liu W, Hu WS, et al. Epidemic characteristics and changing trend of pulmonary tuberculosis in children in Guangzhou City from 2006 to 2020[J]. Chinese Journal of Infection Control, 2021, 20(9): 801-806. |
| [7] |
任正洪. 2005~2011年我国肺结核发病的时间流行病学特征及趋势[J]. 中国卫生统计, 2013, 30(2): 158-161. Ren ZH. The Temporal characteristics and trend of tuberculosis incidence cases in China based on a national surveillance data since 2005[J]. Chinese Journal of Health Statistics, 2013, 30(2): 158-161. |
| [8] |
刘超, 曾芳, 赵紫凤, 等. 呼吸道传染病季节与循环周期特征及预测研究[J]. 中国预防医学杂志, 2021, 22(11): 883-887. Liu C, Zeng F, Zhao ZF, et al. Seasonal and cyclical characteristics and prediction of respiratory infectious diseases[J]. Chinese Preventive Medicine, 2021, 22(11): 883-887. |
| [9] |
李国祥, 李永清, 马天骄. 基于HP滤波法的我国CPI波动规律研究[J]. 经济问题, 2017(10): 60-65, 125. Li GX, Li YQ, Ma TJ. Study on the CPI fuctuations regularity on the basis of HP filter method[J]. On Economic Problems, 2017(10): 60-65, 125. |
| [10] |
Xia YY, Huang F, Chen H, et al. The impact of COVID -19 on tuberculosis patients' behavior of seeking medical care-China, 2020[J]. China CDC Wkly, 2021, 3(26): 553-556. |
| [11] |
李俊, 张云, 刘锦宏, 等. 新冠肺炎疫情对湖北省荆州市结核病控制影响分析[J]. 中国公共卫生, 2022, 38(10): 1340-1344. Li J, Zhang Y, Liu JH, et al. Impact of COVID -19 epidemic on tuberculosis control in Jingzhou city[J]. Chinese Journal of Public Health, 2022, 38(10): 1340-1344. |
| [12] |
中国疾病预防控制中心传染病预防控制处. 2022年8月中国甲乙丙类传染病疫情动态概要[J]. 疾病监测, 2022, 37(9): 1138-1139. Division of Infectious Disease, Chinese Center for Disease Control and Prevention. Summary of national data of class A, B and C communicable diseases in China, August 2022[J]. Di-sease Surveillance, 2022, 37(9): 1138-1139. |
| [13] |
中国疾病预防控制中心传染病预防控制处. 2022年9月中国甲乙丙类传染病疫情动态概要[J]. 疾病监测, 2022, 37(10): 1264-1265. Division of Infectious Disease, Chinese Center for Disease Control and Prevention. Summary of national data of class A, B and C communicable diseases in China, September 2022[J]. Disease Surveillance, 2022, 37(10): 1264-1265. |
| [14] |
Long Q, Guo L, Jiang WX, et al. Ending tuberculosis in China: health system challenges[J]. Lancet Public Health, 2021, 6(12): e948-e953. |
| [15] |
The Lancet Public Health. Public health in China: achievements and future challenges[J]. Lancet Public Health, 2018, 3(10): e456. |
| [16] |
魏珊, 陆一涵, 高眉扬, 等. 中国主要法定报告传染病的"春节效应"研究[J]. 复旦学报(医学版), 2013, 40(2): 153-158. Wei S, Lu YH, Gao MY, et al. "Spring festival effects" on the main notifiable communicable diseases in China[J]. Fudan University Journal of Medical Sciences, 2013, 40(2): 153-158. |
| [17] |
任嘉豪, 徐洁, 杨海燕. ARIMA及Holt-Winters指数平滑模型在河南省肺结核流行趋势预测中的应用[J]. 郑州大学学报(医学版), 2022, 57(6): 756-760. Ren JH, Xu J, Yang HY. Application of ARIMA and Holt-Winters exponential smoothing models in prediction of pulmonary tuberculosis prevalence in Henan province[J]. Journal of Zhengzhou University(Medical Sciences), 2022, 57(6): 756-760. |
| [18] |
Liu MY, Li QH, Zhang YJ, et al. Spatial and temporal clustering analysis of tuberculosis in the mainland of China at the prefecture level, 2005-2015[J]. Infect Dis Poverty, 2018, 7(1): 106. |
| [19] |
GBD 2019 Tuberculosis Collaborators. Global, regional, and national sex differences in the global burden of tuberculosis by HIV status, 1990-2019:results from the global burden of disease study 2019[J]. Lancet Infect Dis, 2022, 22(2): 222-241. |
| [20] |
Orazulike N, Sharma JB, Sharma S, et al. Tuberculosis (TB) in pregnancy-a review[J]. Eur J Obstet Gynecol Reprod Biol, 2021, 259: 167-177. |
| [21] |
Pratiwi IN, Hidayati L, Alviani NI, et al. The correlation between anxiety levels and spiritual activities with motivation to recover in pulmonary tuberculosis[J]. Enfermería Clínica, 2021, 31(Suppl 3): 535-539. |



