2. 西安建筑科技大学力学技术研究院, 陕西 西安 710055;
3. 中国中元国际工程有限公司, 北京 100089;
4. 西安中地工程规划设计有限公司, 陕西 西安 710055
2. Institute of Mechanics and Technology, Xi'an University of Architecture and Technology, Xi'an 710055, China;
3. China IPPR International Engineering CO., LTD., Beijing 100089, China;
4. Xi'an Zhong Di Engineering Planning and Design Corporation, Xi'an 710055, China
二十一世纪以来,世界各地发生了多起重大传染病疫情,造成了惨重的人员伤亡与巨额的财力损失。同时,人们对于传染动力学的研究也在不断发展,以经典的仓室模型为基础不断结合新的方法改进模型,使模拟结果越来越接近真实的疾病传播过程。类比人群动力学的分类方法,已有的传染动力学模型分为宏观和微观两类。宏观模型关注大区域大规模健康状况不同的各类人群数量的变化,忽略个体间感染的细节。微观问题则关注小区域小规模人群中感染的传播情况,重视局部个体间相互作用的影响。宏观模型主要包括经典仓室模型以及部分以复杂网络为基础的传染动力学模型,微观模型主要是考虑个体运动的改进仓室模型,文献调研结果显示微观模型有益于分析具体的感染过程,但仍存在一些值得探讨的方面:(1)元胞自动机用于描述个体运动的规则固定,难以反映更加真实的运动特性和个体间的相互作用。(2)复杂网络多基于社会联系建立,对于陌生个体间的接触描述相对困难。(3)复杂网络中个体运动速度大小的设置多为定值,且忽略了个体间接触时间对感染概率的影响,与真实情况存在差异。
针对上述问题,研究基于能够描述行人个体运动的社会力模型,通过引入感染状态、接触时长和感染概率等因素,对微观人群的感染传播过程进行研究,以典型的公共建筑之一地铁站为例研究人群运动对感染的影响。本研究介绍考虑了个体感染的社会力模型,基于社会力模型对地铁站的感染传播进行模拟,确定主要影响因素。验证增加隔挡设施与改变行人运动特性对降低感染风险的有效性,并对地铁站行人出站过程的防控措施给出建议。
1 物理模型 1.1 考虑个体感染的社会力模型社会力模型是一种离散单元方法,被广泛用于描述行人运动。社会力模型能够更加真实地反映微观个体间的相互作用,对判断行人间的接触过程存在优势。社会力模型[1]基于牛顿第二运动定律,以每一个行人为研究对象,分析其受力,研究人群的运动情况。行人i受力与加速度的关系如式(1)所示:
| ${m_i}\frac{{d{{\vec v}_i}}}{{dt}} = \vec f_i^0 + \sum\limits_{j( \ne 1)} {{{\vec f}_{ij}}} + \sum\limits_w {{{\vec f}_{iw}}} $ | (1) |
行人受到的合力包括三部分,第一部分
| $\vec f_i^0 = {m_i}\frac{{v_i^0(t)\vec e_i^0 - {{\vec v}_i}(t)}}{{{\tau _i}}}$ | (2) |
其中,mi为行人i的质量,
第二部分
| $ \vec{f}_{i j}=\underbrace{A_{i} \exp \left[\left(r_{i j}-d_{i j}\right) / B_{i}\right] \vec{n}_{i j}\left[\lambda_{i}+\left(1-\lambda_{i}\right) \frac{1+\cos \varphi_{i j}}{2}\right]}_{\text {非接触力 }} \\+ \underbrace{k g\left(r_{i j}-d_{i j}\right) \overrightarrow{n_{i j}}+\kappa g\left(r_{i j}-d_{i j}\right) \Delta v_{j i}^{t} \vec{t}_{i j}}_{\text {接触力 }} $ | (3) |
式中Ai和Bi为常数,
第三部分
对于较为复杂的几何空间,社会力模型在确定期望速度方向时较为困难,因此本研究通过格子Boltzmann方法计算流场速度矢量的方式确定行人期望速度的方向[2]。采用D2Q9模型,边界条件设置为反弹边界,为防止涡的出现,采用较小的雷诺数确定初始状态参数,在这里取雷诺数为1。
研究假设感染传播的方式为飞沫传播,参考SEIR给出的人群分类假设个体的健康状况。关于行人的感染判定方法如下:在人群运动的过程中,当易感者与感染者之间的距离≤感染半径,并且保持在该范围内达到一定时间后,即认为与感染者发生了接触。随后系统将生成一个随机数Nrandom,0 < Nrandom < 1,之后对生成的随机数进行判断,如果随机数≤感染概率,则易感者被感染成为潜伏者。最后,成为潜伏者的易感者经过一段时间后转化为感染者。具体行人的感染状态fI可由式(4)确定,fI不同取值如下:0代表易感者,1代表潜伏者,2代表感染者。本研究未考虑移除者(康复者)的存在。
| ${f_I} = \left\{ {\begin{array}{*{20}{l}} {0, \left( {{d_{IS}} > {r_{Inf}}} \right)\bigcup {\left( {{N_{random{\rm{ }}}} > {p_{Inf}}} \right)} \cup \left( {{t_c} < {t_{cl}}} \right)}\\ {1, \left( {{d_{IS}} \le {r_{Inf}}} \right) \cap \left( {{N_{random{\rm{ }}}} \le {p_{Inf}}} \right) \cap \left( {{t_c} \ge {t_{cl}}} \right)}\\ {2, {t_{dely{\rm{ }}}} > {t_{ej}}} \end{array}} \right.$ | (4) |
其中,
以新型冠状病毒肺炎(COVID -19)传播为例,潜伏期约7 d,如基本传染数R0=3时,假设该感染者每次乘坐地铁平均可接触10人,每天乘坐4次地铁,且假设只有地铁内会发生传染,因此7 d内共计接触280人,其中3人被感染,故每次接触的感染概率pInf=3/280=0.010 7。其中每次乘坐地铁的平均接触人数可以由不考虑个体感染的社会力模型在具体的地铁站模拟计算确定,因此对于一个给定的地铁站几何条件和给定的R0,就可以确定感染概率pInf。另外由于潜伏期tei远远大于行人出站所用时间,因此模拟中未考虑潜伏者转化为感染者的情况。但是如果将此模型推广到大范围与大空间的尺度,考虑行人若干天的运动,上式仍然适用。
本模型结合经典社会力模型和距离相关的个体传染模型,能够根据具体的接触时间判定接触,能够模拟行人间、行人建筑间的相互作用,使得微观人群运动感染模拟更接近真实的感染传播过程。
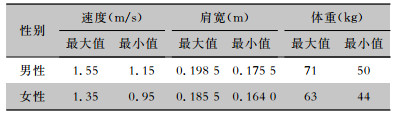
1.2 参数设置参照已有典型地铁站的CAD图纸设置模拟场景(见图 1),-1F为站台层,1F为站厅层,图中标注了主要的相关尺寸。模拟的初始条件设置如下:首先给一定的时间使规则分布于车厢的行人进行小范围的随机运动,之后行人下车步行通过两侧楼梯到达站厅层,到达站厅层后的行人随机选择出口,通过左右两侧闸机从四个出口中的任意一个离开地铁站。初始感染者仅一人,每个算例重复计算300次,经验证重复次数已足够获得稳定的结果,每次计算当中初始感染者在车厢中的位置随机。以下几点需要说明:(1)因为行人出站过程时间较短,假设出站过程中被感染的潜伏者不具有传染性。(2)只考虑行人出站过程,未考虑进出站同时存在的情况。(3)只考虑单侧列车出站过程,未考虑两侧列车同时到站的情况。(4)假设列车上无人停留,行人在列车到站后全部下车。(5)未考虑出站闸机开关时间的影响。(6)行人期望速度取值满足均匀分布[2],个体尺寸依据相关标准取值[4],见表 1。
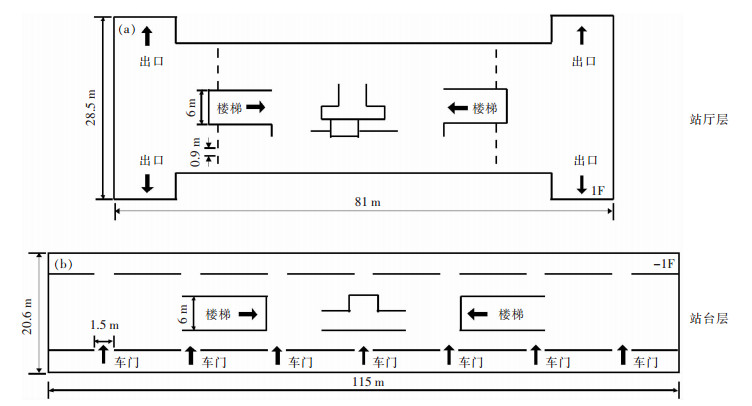 |
| 图 1 模拟场景图 Figure 1 Simulation scene |
| 表 1 行人各项参数取值 Table 1 Values of pedestrian parameters |
|
本研究假设病毒传播的方式为飞沫传播,人与人之间的接触是发生感染的必要条件。首先,对模型的准确性进行验证。根据1.1节的介绍,通过给定场景、人数计算运动过程,可确定平均接触人数,结合假设的R0可估算感染概率。然后使用估算的感染概率计算运动及感染过程,统计计算被感染人数,若与假设的R0值接近,则证明模型准确性满足要求。如图 2所示,假设R0值为50,得到感染概率为0.101,利用此感染概率模拟运动及感染过程,统计被感染人数(即反映为R0值)。可以看到在算例重复次数达到300之后,模拟结果与假设的R0一致且保持不变。因此模型的准确性能满足要求,且算例重复计算300次可得到稳定的结果。验证模拟中是7 d,共28次出站情况下的感染人数,后续的模拟计算中只进行1次出站过程的模拟,重复300次求平均值。
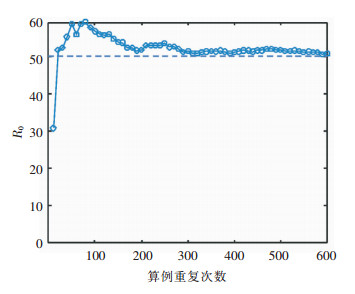 |
| 图 2 R0模拟结果与算例重复次数的关系 Figure 2 Relationship between simulation result of R0 and number of repetitions of the calculation example |
模拟不同出站总人数的情况下,接触次数以及感染人数的变化。模拟参数[5]设置如下:感染半径1.5 m,感染概率0.101。其中R0=50,大于文献中的取值,目的是为呈现更明显的感染人数的变化。将此算例作为对照组,便于之后模拟结果的对照分析。随着出站总人数的增加,行人间的接触次数和感染人数均增大。对比两条曲线可见在相同的参数设置条件下,接触次数结果的波动范围更大,见图 3(a)。可能是行人具有跟随效应[6]的缘故,由于跟随效应的存在,被感染者多为初始感染者周围的行人,因此初始感染者的位置会对感染人数产生重要的影响。为了验证,统计距离初始感染者不同位置处被感染的人数,获得距离感染率,即不同距离处被感染的概率,初始位置与感染者越接近,被感染的概率越大,见图 3(b)。
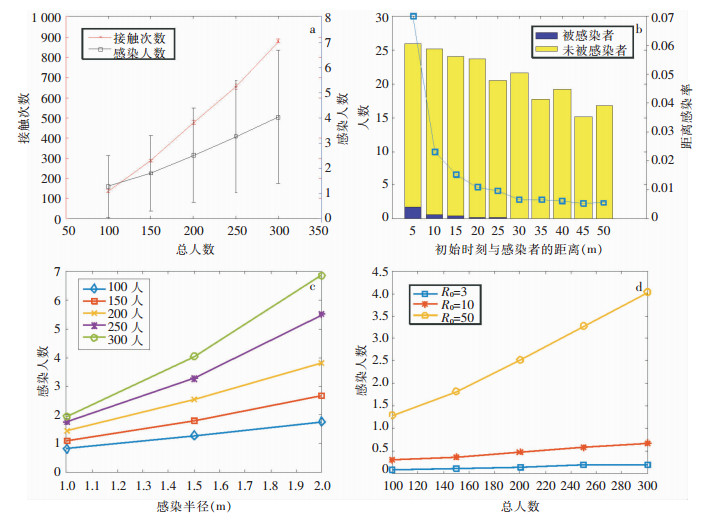 |
| a:接触次数和感染人数随出站总人数的变化;b:感染概率与初始感染者距离的关系;c:感染人数随感染半径的变化;d:基本传染数R0不同时,感染人数的变化。 图 3 模拟不同状态下地铁站内人员感染情况 R0=3, pInf=0.006; R0=10, pInf=0.020; R0=50, pInf=0.101 Figure 3 Simulating the infection of persons in subway station under different conditions |
为有针对性地提出防控措施,首先需要确定主要的影响因素,分别模拟不同感染半径以及基本传染数下的感染情况。结果显示,无论何种情况下,感染人数均随着出站总人数的增加而增大,较大的人群密度会促进感染传播。对比感染半径与基本传染数的变化对感染人数的影响,发现感染半径的影响程度更大,见图 3(c、d)。感染半径、出站总人数对感染传播存在显著影响,防控措施的制定考虑从以上两个方面入手,如控制进站人数,降低人群的聚集程度以及增大行人间距等。
2.1 地铁站内行人聚集分析观察地铁站中几个主要位置的人群聚集情况。由于站台层空间有限,行人目的地相对一致,因此聚集现象较为严重,从不同车门下车的行人在楼梯口处聚集,见图 4(a)。之后,在通过楼梯的过程中,行人之间在较长的一段时间里一直保持着相对小的距离,见图 4(b)。而站厅层空间开阔,行人目的地不同,行人随机向四个出口方向分流,聚集现象不明显,见图 4(c)。虽然存在对向人流的交叉混合,但是由于接触时间较短因此感染的可能性相对较小。所以感染主要发生在站台层,行人同向行进且间距较小接触时间较长,楼梯处是行人发生聚集的主要位置。如图 4(d)所示为感染密度图,rho值的大小表示单位面积被感染者的个数,图上结果为300次重复计算叠加的效果,可见楼梯处感染人数较多。接下来模拟楼梯处设置隔挡设施的场景,比较结果以获得合理的隔挡方式。
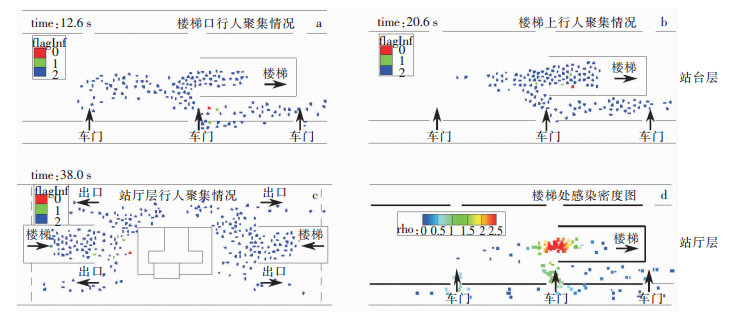 |
| 图 4 地铁站内主要位置人群聚集情况 Figure 4 Crowd gathering at main locations of subway station |
地铁站中经常会设置活动栏杆、伸缩栏杆和铁马等隔挡设施,用来引导行人流,尤其在客流量高峰期,隔挡设施起到了提高效率、缓解拥堵的重要作用。利用隔挡的方式分散人流,可以减少出站行人的接触次数,降低感染人数,如设置楼梯隔挡。楼梯原有宽度为6.0 m,通过设置隔挡的方式将其划分为狭窄通道,模拟通道宽度分别为1.2、1.5、2.0 m的地铁人员感染情况,结果显示:人数较少通道宽度为1.5 m时减少感染人数的效果较为明显;随着总出站人数的增多,通道宽度为2.0 m时更有利于感染人数的降低;随着总人数的进一步增大,降低感染人数效果的整体趋势变差,见图 5(a)。对照组与措施组感染密度图对比可见,楼梯加隔挡后大大降低了楼梯口处的感染人数,见图 5(b)。在人数≤200人的情况下,措施组感染人数与对照组相比降低了23%。
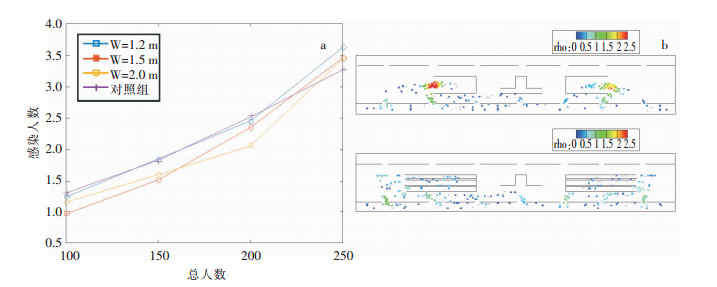 |
| a:楼梯加隔挡后的感染情况;b:对照组的感染密度图与楼梯加隔挡后的感染密度图,以通道宽度1.5 m为例。 图 5 设置楼梯隔挡地铁站内行人感染情况及感染密度图 Figure 5 Infection situation and infection density of pedestrians in subway station with stair barrier |
社会力模型中的参数Bi表示个体对于其他行人的社会排斥力特征长度,值越大则代表行人之间的排斥力越大,如式(3)所示,相应行人间的间距越大。因此,若要增大行人间距只需增大Bi值,结果显示增大行人间距能够显著降低感染人数;在出站总人数为300人的情况下,增大行人间距后感染人数降低25%,见图 6(a)。由子图可见,随着行人间距的增大,楼梯处行人密度减小,说明聚集程度降低。
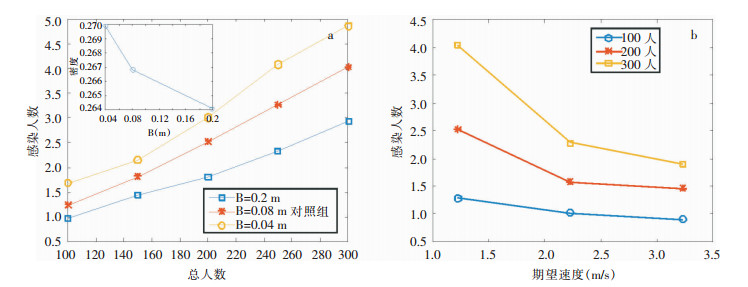 |
| a:行人间距变化对感染的影响; 子图为不同行人间距的情况下,楼梯处行人密度的变化,以总人数150人为例。b:不同期望速度下的感染人数。 图 6 地铁站行人间距变化及期望速度对感染的影响 Figure 6 Effects of subway station pedestrian distance and expected speed on infection |
增大行人间距的方法有效减少了感染人数,但在人流高峰期,较大的行人间距很难保证。因为地铁站空间有限,人流量的增多使得行人间的距离减小。期望速度值的大小反映行人想要到达出口意愿的强烈程度,期望速度越大则行人实际的移动速度越大。因此,采用期望速度的大小反映行人移动速度的变化。模拟期望速度变化对感染人数的影响,结果显示,随着期望速度的增加感染人数降低,尤其在出站总人数较多时降低的趋势更明显。在出站总人数300人的情况下,增大期望速度降低了50%的感染人数,见图 6(b)。
3 讨论宏观模型主要包括经典仓室模型以及部分以复杂网络为基础的传染动力学模型,如COVID -19疫情期间,研究人员基于SEIR模型对疫情的发展情况进行预测[7-11]。Li等[12]结合SEIR模型和城市交通网络模型,提出一个适用于中国城市流行病传播的模拟系统,通过与官方数据的拟合验证了模型的可靠性。结合复杂网络的传染分析以静态网络为主,即假设网络中节点间的联系在时间上保持不变。研究人员[13-14]以仓室模型为基础,分别引入了间接感染率和非均匀传播,结果表明降低间接感染率以及非均匀传播能够降低感染风险,两个研究对复杂网络模型中的等概率感染相邻节点的假设进行了改进,使模拟更加接近实际情况。微观模型主要是考虑个体运动的改进仓室模型,如与元胞自动机[15]、复杂网络[16]结合的传染研究,另外还包括利用社会力模型描述感染传播的研究。经典仓室模型忽略了个体间接触概率的差异,遵循均匀混合假设,研究[17-18]对此进行改进,引入个体运动和感染半径的因素,分别验证长程运动概率以及运动形式限制对感染传播的影响,结果表明长程运动会加速感染传播,而运动形式限制能够降低感染风险。周海平等[19]结合元胞自动机和SIS模型研究感染传播,结果表明人群的流动会很大程度上加速感染的传播,感染风险随人群密度的增大而增大。于红等[20]基于复杂网络理论研究不同易感性、感染性、个体运动以及感染周期的影响,得到并验证了传播阈值的表达式。Namilae等[3]基于社会力模型,模拟飞机登机和离机过程中乘客之间的接触对感染传播的影响,评估不同的登机、离机方式等对接触次数的影响。
针对微观模型存在的问题,本研究基于能够描述行人个体运动的社会力模型,通过引入感染状态、接触时长和感染概率等因素,以典型的公共场所地铁站为例,研究微观人群中个体运动对感染传播的影响,分析多种防控措施的有效性,结果表明:(1)楼梯隔挡能够在一定程度上降低感染人数,但合适的通道宽度需要根据实际情况设置,太宽的通道无法达到减轻聚集程度的目的,而通道过窄则会影响通行能力,有可能造成拥堵,增大接触时间促进感染传播。楼梯隔挡的存在起到了分散人流的作用,降低了行人间的接触次数。(2)随着总人数的增加,楼梯隔挡措施有效性下降,因为随着人数的增多,通道的通行能力下降,行人间接触时间增长。同时站厅层对向行人流接触次数增多,感染人数增多。(3)增大行人间距,能够减少感染半径范围内的易感者人数,增大期望速度降低了行人间的接触时间,两者均可显著降低感染人数。因此,可通过地铁站广播、绘制标识线、工作人员监督等方式引导行人自觉保持间距,尽快出站。(4)出站总人数的增加会导致防控措施有效性降低,因此,除了做好特殊时期的测温筛查工作,还应注意进站人数的控制,才能保证防控措施的合理有效性。
致谢: 感谢李安桂教授对文章提出的建设性意见。
| [1] |
Helbing D, Molnár P. Social force model for pedestrian dynamics[J]. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics, 1995, 51(5): 4282-4286. |
| [2] |
Korhonen T, Hostikka S. Fire dynamics simulator with evacuation: FDS+Evac: technical reference and user's guide[EB/OL]. [2021-05-04]. https://www.vttresearch.com/sites/default/files/pdf/workingpapers/2009/W119.pdf.
|
| [3] |
Namilae S, Srinivasan A, Mubayi A, et al. Self-propelled pedestrian dynamics model: application to passenger movement and infection propagation in airplanes[J]. Physica A, 2017, 465: 248-260. DOI:10.1016/j.physa.2016.08.028 |
| [4] |
国家技术监督局. 中国成年人人体尺寸: GB 10000-1988[S]. 北京: 中国标准出版社, 1989. The State Bureau of Quality and Technical Supervision. Human dimensions of Chinese adults: GB 10000-1988[S]. Beijing: Standards Press of China, 1989. |
| [5] |
潘海啸, 崔毅. 基于微观仿真出行模型的病毒时空扩散分布与控制[J]. 城市交通, 2020, 18(3): 62-70. Pan HX, Cui Y. Virus spatiotemporal diffusion distribution and control based on micro simulation travel model[J]. Urban Transport of China, 2020, 18(3): 62-70. |
| [6] |
杨晓霞. 基于社会力模型的地铁枢纽站行人流动态特性与疏散研究[D]. 北京: 北京交通大学, 2017. Yang XX. Pedestrian flow dynamic characteristics and evacuation in the metro hub station based on the social force model[D]. Beijing: Beijing Jiaotong University, 2017. |
| [7] |
Aleta A, Moreno Y. Evaluation of the potential incidence of COVID -19 and effectiveness of containment measures in Spain: a data-driven approach[J]. BMC Med, 2020, 18(1): 157. DOI:10.1186/s12916-020-01619-5 |
| [8] |
Zhou XK, Wu ZG, Yu RR, et al. Modelling-based evaluation of the effect of quarantine control by the Chinese government in the coronavirus disease 2019 outbreak[J]. Sci China Life Sci, 2020, 63(8): 1257-1260. DOI:10.1007/s11427-020-1717-9 |
| [9] |
Su LX, Hong N, Zhou X, et al. Evaluation of the secondary transmission pattern and epidemic prediction of COVID -19 in the four metropolitan areas of China[J]. Front Med (Lausanne), 2020, 7: 171. |
| [10] |
Shao P, Shan YJ. Beware of asymptomatic transmission: study on 2019-nCoV prevention and control measures based on extended SEIR model[J]. bioRxiv, 2020. DOI: 10.1101/2020.01.28.923169. Epub ahead of print.
|
| [11] |
Pan JH, Ye Y, Liu ZX, et al. Effectiveness of control strategies for Coronavirus Disease 2018: a SEIR dynamic modeling study[J]. Bull World Health Organ, 2020. DOI: 10.2471/BLT.20.253807. Epub ahead of print.
|
| [12] |
Li TY. Simulating the spread of epidemics in China on multi-layer transportation networks: beyond COVID -19 in Wuhan[J]. Europhys Lett, 2020, 130(4): 48002. DOI:10.1209/0295-5075/130/48002 |
| [13] |
陈仁霞, 李士生, 高冉. 复杂网络上具有免疫接种的L-SIRS流行病模型研究[J]. 数学的实践与认识, 2015, 45(8): 307-311. Chen RX, Li SS, Gao R. L-SIRS epidemic model with immunization on complex networks[J]. Mathematics in Practice and Theory, 2015, 45(8): 307-311. |
| [14] |
赵敬, 夏承遗, 孙世温, 等. 复杂网络上同时考虑感染延迟和非均匀传播的SIR模型[J]. 智能系统学报, 2013, 8(2): 128-134. Zhao J, Xia CY, Sun SW, et al. A novel SIR model with infection delay and nonuniform transmission in complex networks[J]. CAAI Transactions on Intelligent Systems, 2013, 8(2): 128-134. |
| [15] |
郑三强, 韩晓卓. 多因素制约下的SIR传染病模型的元胞自动机仿真模拟研究[J]. 广东工业大学学报, 2018, 35(5): 51-59. Zheng SQ, Han XZ. A simulation of cellular automata based on the SIR infectious disease model with multifactorial constraints[J]. Journal of Guangdong University of Technology, 2018, 35(5): 51-59. DOI:10.3969/j.issn.1671-623X.2018.05.006 |
| [16] |
夏承遗, 马军海, 陈增强. 复杂网络上考虑感染媒介的SIR传播模型研究[J]. 系统工程学报, 2010, 25(6): 818-823. Xia CY, Ma JH, Chen ZQ. SIR epidemic model with infection medium on complex networks[J]. Journal of Systems Engineering, 2010, 25(6): 818-823. |
| [17] |
夏承遗, 孙世温, 孙俊清, 等. 考虑个体运动的SIS传染模型研究[J]. 自然科学进展, 2009, 19(9): 999-1003. Xia CY, Sun SW, Sun JQ, et al. On the SIS model with individuals motion[J]. Progress in Natural Science, 2009, 19(9): 999-1003. DOI:10.3321/j.issn:1002-008X.2009.09.014 |
| [18] |
赵敬, 方义, 夏承遗. 考虑个体移动和局域控制的SIR传染模型[J]. 智能系统学报, 2011, 6(6): 515-519. Zhao J, Fang Y, Xia CY. A susceptible-infected-removed model considering individual mobility and local control[J]. CAAI Transactions on Intelligent Systems, 2011, 6(6): 515-519. DOI:10.3969/j.issn.1673-4785.2011.06.006 |
| [19] |
周海平, 蔡绍洪. 个体运动的病毒传播行为模拟[J]. 现代生物医学进展, 2008, 8(11): 2182-2183, 2190. Zhou HP, Cai SH. The simulation of virus spreading based on moving individuals[J]. Progress in Modern Biomedicine, 2008, 8(11): 2182-2183, 2190. |
| [20] |
于红, 李科赞, 贾荣, 等. 带受限感染周期的随机移动传播网络阈值分析[J]. 桂林电子科技大学学报, 2014, 34(5): 426-430. DOI:10.3969/j.issn.1673-808X.2014.05.018 |



