2020年新型冠状病毒肺炎疫情暴发,大量人员感染死亡,并给全球经济造成了巨大损失。新型冠状病毒可在空气中存活3 h,同时可通过气溶胶传播[1-2]。气溶胶指气溶胶颗粒、液滴核等在空气中的悬浮液[3],空气中的颗粒易吸附细菌与病毒,被人体吸入后可能会导致感染[4]。人们一天90%的时间都呆在室内,长期暴露在室内颗粒物污染环境中,将对人体健康产生影响[5]。
人在咳嗽、打喷嚏时,大量的飞沫可能会携带病菌从人体口腔和鼻腔释放,随室内气流运动,通过口腔、呼吸道等方式侵入人体,导致人体感染疾病[6]。2020年11月,天津某小区接连出现8例新型冠状病毒感染者,经调查发现,小区首个感染者曾乘坐电梯时未佩戴口罩,并在电梯中咳嗽、打喷嚏,污染了电梯环境,最终导致新型冠状病毒在小区内传播。电梯具有封闭性、空间狭小、人员聚集的特点[7],是日常生活中呼吸系统疾病传播的危险场所。携带病菌的飞沫核传播对人的影响主要取决于飞沫核的浓度以及人员处于该环境的时间长短[8],为预防呼吸系统疾病的传播,有必要对不同通风方式下电梯轿厢内的飞沫核扩散展开研究,通过具体分析飞沫核的运动情况、浓度变化以及人员风险,为相关电梯场景下疾病的预防与通风设计提供指导意见。
1 对象与方法 1.1 研究对象对某品牌常用的载重量800 kg,规格为10人的电梯进行研究。假设人员乘坐电梯到达高楼层,在电梯内停留约10 s的时间,通过研究电梯内后部通风、两侧通风、四角通风三种不同通风情况下,人员咳嗽飞沫的扩散运动,比较三种方式下气流速度分布情况、飞沫核的浓度变化,并对通风效果进行评估。选取拟合效果较好的Realizable k-ε紊流模型模拟室内气流运动,同时应用颗粒轨道模型研究人员咳嗽产生的飞沫核在10 s内的扩散运动过程。
1.2 电梯几何模型轿厢内部结构:深度(X)为1 400 mm,宽度(Y)为1 350 mm,高度(Z)为2 350 mm。顶棚设置进风口,其中四角通风的进风口为规格100 mm×100 mm的正方形通风口(1~4);两侧通风方式为400 mm×40 mm的长方形通风口(5、7);后部通风设置一个400 mm×40 mm的长方形通风口(6),电梯门缝作为出风口(8),规格为20 mm×2 350 mm。电梯内四周均匀分布4人。人员电梯模型见图 1。人员D位于飞沫释放者A的正对面,人员C在D旁,人员B则在飞沫释放者A的邻位。
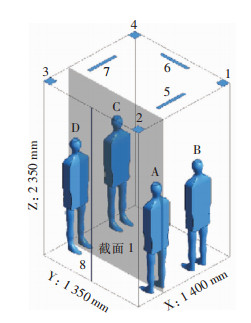 |
| 1~7:分别为进风口1~7;8:出口;A~D:分别为人员A~D。 图 1 电梯和人员几何模型图 Figure 1 Geometry model diagram of elevator and personnel |
本研究主要考虑的是粒径为1 μm的咳嗽飞沫颗粒物。室内气流一般为不可压缩的湍流流动[9],在电梯内部不考虑温度的变化,即流体的温度和密度不改变,将飞沫颗粒物随气流的流动视为气固两相流。飞沫核扩散运动会随时间变化,则对其进行瞬态模拟。在飞沫核扩散过程中,电梯内部的气流遵循湍流状态下质量守恒方程、动量守恒方程,不考虑电梯内部温度变化,则忽略飞沫核的能量变化。流动过程控制方程如下:
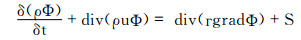
|
(1-1) |
式中,Φ为通用变量,可以代表u、v、w、T等求解变量;г为广义扩散系数;S为广义源项。在Realizable k-ε模型中,关于k与ε的运输方程如下:
| $ \left. {\frac{{{\rm{ \mathsf{ δ} }}({\rm{ \mathsf{ ρ} k}})}}{{{\rm{ \mathsf{ δ} t}}}} + \frac{{{\rm{ \mathsf{ δ} }}\left( {{\rm{ \mathsf{ ρ} k}}{{\rm{u}}_{\rm{i}}}} \right)}}{{{\rm{ \mathsf{ δ} }}{{\rm{x}}_{\rm{i}}}}} = \frac{{\rm{ \mathsf{ δ} }}}{{{\rm{ \mathsf{ δ} }}{{\rm{x}}_{\rm{i}}}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{{\rm{ \mathsf{ σ} }}_{\rm{k}}}}}} \right)\frac{{{\rm{ \mathsf{ δ} k}}}}{{{\rm{ \mathsf{ δ} }}{{\rm{x}}_{\rm{j}}}}}} \right)} \right] + {{\rm{G}}_{\rm{K}}} - {\rm{ \mathsf{ ρ} \mathsf{ ε} }} $ | (1-2) |
| $ \begin{array}{l} \left. {\frac{{{\rm{ \mathsf{ δ} ( \mathsf{ ρ} \mathsf{ ε} )}}}}{{{\rm{ \mathsf{ δ} t}}}}{\rm{ + }}\frac{{{\rm{ \mathsf{ δ} }}\left( {{\rm{ \mathsf{ ρ} \mathsf{ ε} }}{{\rm{u}}_{\rm{i}}}} \right)}}{{{\rm{ \mathsf{ δ} }}{{\rm{x}}_{\rm{i}}}}}{\rm{ = }}\frac{{\rm{ \mathsf{ δ} }}}{{{\rm{ \mathsf{ δ} }}{{\rm{x}}_{\rm{j}}}}}\left[ {\left( {{ {μ + }}\frac{{{{ {μ }}_{\rm{t}}}}}{{{{\rm{ \mathsf{ σ} }}_{\rm{k}}}}}} \right)\frac{{{\rm{ \mathsf{ δ} \mathsf{ ε} }}}}{{{\rm{ \mathsf{ δ} }}{{\rm{x}}_{\rm{j}}}}}} \right)} \right]{\rm{ + \mathsf{ ρ} }}{{\rm{C}}_{\rm{1}}}{\rm{E \mathsf{ ε} - \mathsf{ ρ} }}{{\rm{C}}_{\rm{2}}}\\ \frac{{{{\rm{ \mathsf{ ε} }}^{\rm{2}}}}}{{{\rm{kk + }}\sqrt {{\rm{v \mathsf{ ε} }}} }} \end{array} $ | (1-3) |
其中,σk=1.0;σε=1.2;C2=1.9;C1=max
采用拉格朗日法,通过求解颗粒物运动方程计算单个颗粒物的轨迹。单个颗粒的运动方程可由牛顿第二定律获得:
| $ \frac{{{\rm{d}}{{\rm{u}}_{\rm{p}}}}}{{{\rm{dt}}}} = {{\rm{F}}_{\rm{D}}}\left( {{\rm{u}} - {{\rm{u}}_{\rm{p}}}} \right) + \frac{{{\rm{g}}\left( {{{\rm{ \mathsf{ ρ} }}_{\rm{p}}}{\rm{ - \mathsf{ ρ} }}} \right)}}{{{{\rm{ \mathsf{ ρ} }}_{\rm{p}}}}} $ | (1-4) |
其中:FD(u-up)表示单位质量颗粒所受流体曳力;
人员A口腔部位(嘴唇1)为飞沫释放位置,一次咳嗽约需要0.5 s[11]才能释放出飞沫,则设置0.5 s的稳态模拟,后9.5 s飞沫核随气流的运动轨迹将随时间变化。电梯运行速度1 m/s,向上或下加速度为0.5 m/s2[12],飞沫核以22 m/s[13]与水平夹角约30°斜释放,划分成水平速度19 m/s,垂直速度11 m/s。电梯启动加速时间约为1 s,由于垂直方向加速度小,垂直方向上1 s内速度仅仅变化0.5 m/s,相对于11 m/s可以忽略不计。将唾液看成颗粒物,密度为1 003 kg/m3[14],电梯匀速运动时,颗粒物自身速度在0.01 s内速度可降低至0.000 05 m/s[15],随后颗粒物随气流运动。空调风速相对于电梯设置为2 m/s。室内温度保持不变,电梯出口边界条件设置为-10 Pa。
1.5 网格划分与方程离散求解应用Ansys ICEM进行网格划分[16],在人体表面和四周墙壁等各壁面划分边界层网格,网格元素总数为124万,网格质量均为0.3以上,在缝隙等部位进行局部加密,见图 2。黑色密集部位采用有限体积法建立离散方程,SIMPLE算法是计算不可压缩流场的主要方法,因此选择SIMPLE算法对离散方程组进行求解[17]。
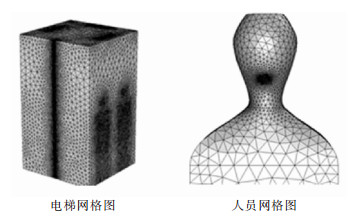 |
| 图 2 电梯模型网格图 Figure 2 Grid diagram of elevator model |
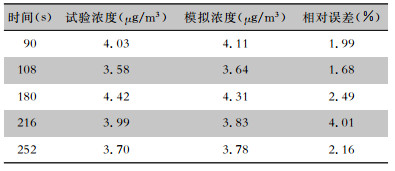
为验证颗粒轨道模型对室内空间飞沫传输过程仿真的适用性和科学性,基于几何相似原理和动力相似原理[18],参照一教学教室尺寸,在实验室内,搭建了一个500 mm×600 mm×350 mm的玻璃小室(见图 3),并在入口处以2.4 m/s的速度注入颗粒物,利用DUSTMATE仪器测量小室内可吸入颗粒物的浓度(PM1),同时建立1∶1的仿真模型,选取74万网格的小室模型,应用颗粒轨道模型进行模拟仿真,最后比较两者的浓度监测值。将颗粒浓度的监测值与模拟计算值进行比较,见表 1,相对误差均小于5%。本研究建立的数值计算模型具有科学性和适用性,可用于研究电梯内飞沫核的扩散运动。
 |
| 图 3 实验装置图 Figure 3 Experimental device |
| 表 1 颗粒浓度的监测值与模拟计算值比较 Table 1 Comparison between monitored and simulated va-lues of particle concentration |
|
通风方式不同,飞沫核的运动方向、沉积速度、不同位置浓度等也会有一定的差异,通过研究轿厢内空气流动的方向,速度大小可以分析飞沫核的扩散运动,并根据飞沫核浓度对通风效果进行评价。
2.1.1 轿厢气流流场分析截取研究截面1(飞沫释放者A与其正对面人员D所在平面,见图 1。研究三种通风方式在不同时刻的速度分布情况,截面1速度矢量图见图 4。比较同一时刻不同通风方式:根据速度标尺可以判断速度大小位置分布,同一时刻后部与四角通风速度大小较为均匀,两侧通风较大风速集中在人员A附近。比较同一通风方式的速度方向以及产生的速度旋涡数量:均随时间发生变化,三种通风方式速度方向总体由上往下再往上,后部通风所产生的速度旋涡数由3个变为2个,且位置下移;两侧通风旋涡数由4个变为3个,集中在电梯中间部位;四角通风旋涡数随时间逐渐增多,电梯顶部和底部各分布2个。
 |
| 图 4 三种通风情况不同时刻截面1速度矢量图 Figure 4 Velocity vector diagram of section 1 at different times under three ventilation conditions |
选取6个时间点,研究10 s内三种通风方式下电梯飞沫核扩散情况,蓝色颗粒代表飞沫核,见图 5。后部通风:飞沫由人员A到达人员D后,先向下运动,再由右下到左上呈倒“S”型路径进行扩散;两侧通风:飞沫核到达人员D后向下,之后经右下再向上运动;四角通风:飞沫核到达人员D后,飞沫核由中间向上下两方向运动,到达电梯顶部与底部后,再向人员A一侧运动呈“C”型趋势。在第5 s时,三种通风方式的飞沫聚集位置及数量已有明显差异,后部及两侧通风的方式飞沫聚集在电梯中下部,而四角通风聚集在电梯一侧,且悬浮数量较少。
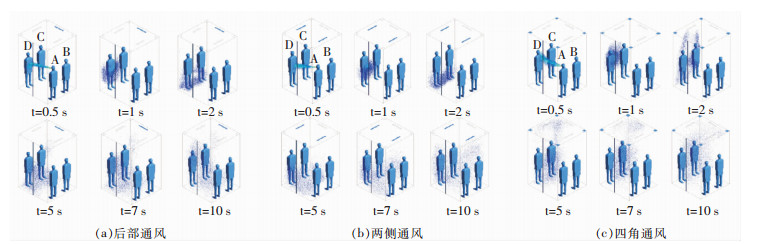 |
| 图 5 三种通风情况下10 s内电梯飞沫扩散特征 Figure 5 Droplet diffusion characteristics within 10 seconds under three ventilation conditions |
由扩散图 5可知,飞沫由人员A释放后,集中在人员D一侧。现选取截面1,分析同一时刻不同通风方式下的浓度差异,见图 6。0.5 s时,在后部及两侧通风方式下,释放的飞沫核集中在人员腹部及以下;在四角通风方式下,飞沫核集中在面部区域,人员接触飞沫颗粒物的风险较大。5 s时,后部通风方式下,飞沫核集中在人员之间的中间位置;两侧通风方式下,飞沫核位于电梯下部,截面处两者的平均飞沫浓度分别集中在7.2×10-10 kg/m3和9.7×10-10 kg/m3左右;四角通风方式下,人员D后靠墙面聚集较多的飞沫核,平均浓度约为4.9×10-10kg/m3,较前两者浓度分别降低了68%和51%左右。10 s时,在后部及两侧通风方式下,飞沫核分别集中在电梯上部、人员D周边;而在四角通风方式下,飞沫核集中区域已不明显。在不同时刻同一通风方式下,三者飞沫核浓度的最高值均逐渐变小,其中四角通风方式下,飞沫浓度变化最明显,在10 s时,飞沫核的平均浓度已集中在5.4×10-10 kg/m3左右,但在10 s时,平均浓度存在增加的现象。
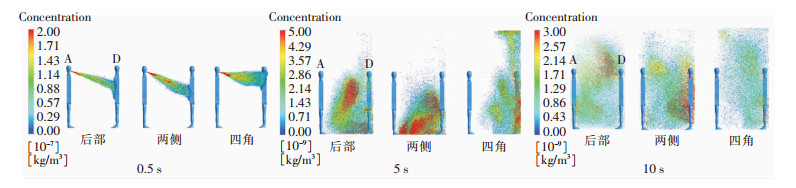 |
| 图 6 三种通风情况下不同时刻截面1浓度分布图 Figure 6 Concentration distribution diagram of section 1 at different times under three ventilation conditions |
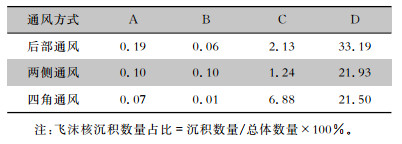
研究不同通风方式下,飞沫核浓度对轿厢内人员的影响,将飞沫颗粒物沉积数量作为人员接触风险指标,以此比较人员的接触风险大小,同时以悬浮量作为人员吸入风险指标。10 s时三种通风情况下人员飞沫核的沉积数量占比情况:人员D在10 s时飞沫核沉积数量占比最高,接触飞沫核的风险最大,人员C次之,人员B占比均在0.1%以下,风险相对较小。10 s时,后部通风情况下,人员D占比达33.19%,人员C则占比2.13%;两侧通风情况下,人员D占比21.93%,人员C占比亦在1.24%;四角通风情况下,人员D飞沫核沉积数量占比达21.50%,人员C次之,飞沫核沉积量占比6.88%。在四角通风情况下,相比后部通风人员D接触飞沫的风险有所降低,而人员C接触飞沫颗粒物的风险显著增加。见表 2。
| 表 2 10 s时三种通风下人员飞沫核的沉积数量占比(%) Table 2 Proportion of the deposition number of person's droplet nuclei at second 10 under three ventilation conditions (%) |
|
10 s时三种通风情况下电梯轿厢内飞沫核悬浮数量:在四角通风情况下,颗粒物悬浮量最小,相比两侧通风情况,悬浮量下降31%,相比后部通风下降12%。但对比后部通风与两侧通风情况,随通风量增加,颗粒物的悬浮量并未显著下降,两侧通风情况比后部通风增加27%,人员风险也相应增加。见表 3。
| 表 3 10 s时三种通风情况下电梯轿厢内颗粒物沉积悬浮数量 Table 3 Contents of suspension and deposition of particles in elevator at second 10 under three ventilation conditions |

|
郑聪[19]应用Fluent软件,证明Realizable k-ε紊流模型对室内气流模拟具有良好的科学性和适用性,因此本研究选取Realizable k-ε紊流模型模拟室内气流运动,同时应用颗粒轨道模型研究某人员咳嗽产生的飞沫核在10 s内的扩散运动过程。研究主要考虑的是粒径为1 μm的咳嗽飞沫颗粒物,原因是飞沫为含有少量固体小颗粒的小液滴,其粒径97%约在0.5~12 μm[20],水分完全蒸发后约为1 μm左右[21],由于蒸发时间短,研究时可以将其蒸发时间忽略不计[22],小粒径的飞沫会随气流运动,被人体吸入,可能会造成呼吸系统疾病,危险性大。
飞沫核在室内主要随气流运动,良好的通风组织,可以帮助室内形成良好的清洁环境。Zhang等[23]采用数值模拟方法研究高速铁路旅客舱内呼吸性雾滴的扩散过程,结果表明,当从前门到后门有气流时,雾滴扩散更远,对旅客的影响更大。
模拟三种通风方式下的飞沫核运动,经过分析处理,得出以下结论:(1) 在其他条件相同的情况下,不同的通风方式所产生的气流旋涡数量及位置分布有所差异,后部通风和两侧通风的旋涡数量随时间逐渐减少,而四角通风情况下,逐渐增加。飞沫核整体将随气流由上到下再到上运动,由于速度旋涡不一样,飞沫核扩散将产生不一样的运动轨迹,各位置的飞沫核浓度也有所差异。(2) 气流旋涡数量和位置的不同,使三种通风方式下,飞沫核的运动轨迹产生差异,后部通风情况下飞沫核随气流呈现倒“S”型轨迹运动,两侧通风时飞沫核随气流上下运动,四角通风则呈现“C”型轨迹。不同的速度旋涡会引起飞沫核扩散方向产生差异,当旋涡位置恰当时,可以有效地将飞沫带离人员附近,且可以有效稀释局部飞沫浓度;位置不恰当时,将会增加人员接触飞沫颗粒物的风险。由后部通风至四角通风,通风速度不变,随着通风口总体面积增加,通风量逐渐增加,飞沫核被稀释的效果明显,相同时间内人员吸入飞沫颗粒物的风险逐渐降低。(3) 在截面1对飞沫浓度进行分析,结果表明:经过10 s时间,后部通风、两侧通风、四角通风方式下,随着通风量的增加,飞沫稀释效果明显,10 s内飞沫核浓度可以减少90%以上,相同时间内人员吸入飞沫颗粒物的风险逐渐降低。因此合理增加通风量可以有效稀释飞沫浓度,改善空气质量。(4) 在三种通风方式下,飞沫释放者A的对立面,为接触携带病菌飞沫的高风险区,四角通风能够快速稀释飞沫浓度,但人员C在该方式下,飞沫核沉积量占比达7%,接触飞沫风险显著增加,由此在有效稀释飞沫浓度的同时,还应注意通风口位置分布,减少人员接触飞沫风险。
| [1] |
Morawska L, Cao J. Airborne transmission of SARS -CoV-2:the world should face the reality[J]. Environ Int, 2020, 139: 105730. DOI:10.1016/j.envint.2020.105730 |
| [2] |
van Doremalen N, Bushmaker T, Morris DH, et al. Aerosol and surface stability of SARS -CoV-2 as compared with SARS -CoV-1[J]. N Engl J Med, 2020, 382(16): 1564-1567. DOI:10.1056/NEJMc2004973 |
| [3] |
Vuorinen V, Aarnio M, Alava M, et al. Modelling aerosol transport and virus exposure with numerical simulations in relation to SARS -CoV-2 transmission by inhalation indoors[J]. Saf Sci, 2020, 130: 104866. DOI:10.1016/j.ssci.2020.104866 |
| [4] |
MØlhave L, Schneider T, Kjærgaard SK, et al. House dust in seven Danish offices[J]. Atmos Environ, 2000, 34(28): 4767-4779. DOI:10.1016/S1352-2310(00)00104-7 |
| [5] |
Li ZS, Wen QM, Zhang RL. Sources, health effects and control strategies of indoor fine particulate matter (PM2.5): a review[J]. Sci Total Environ, 2017, 586: 610-622. DOI:10.1016/j.scitotenv.2017.02.029 |
| [6] |
Gralton J, Tovey E, McLaws ML, et al. The role of particle size in aerosolised pathogen transmission: a review[J]. J Infect, 2011, 62(1): 1-13. DOI:10.1016/j.jinf.2010.11.010 |
| [7] |
范奉和, 李启文, 廖志强. 新冠肺炎疫情之下的电梯通风技术研究[J]. 中国电梯, 2020, 31(8): 23-27. Fan FH, Li QW, Liao ZQ. Research on ventilation technology of elevator in the epidemic situation of COVID -19[J]. China Elevator, 2020, 31(8): 23-27. |
| [8] |
刘树森. 口腔散发微生物气溶胶在室内传播和运动规律的研究[D]. 天津: 天津大学, 2007. Liu SS. Study on transport mechanisms of bio-aerosol produced by mouth in the indoor environment[D]. Tianjin: Tian-jin University, 2007. |
| [9] |
Kang ZQ, Zhang YX, Fan HB, et al. Numerical simulation of coughed droplets in the air-conditioning room[J]. Procedia Eng, 2015, 121: 114-121. DOI:10.1016/j.proeng.2015.08.1031 |
| [10] |
陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001. Tao WQ. Numerical heat transfer[M]. Second edition. Xi'an: Xi'an Jiaotong University Press, 2001. |
| [11] |
Zhang YX, Feng GH, Bi Y, et al. Distribution of droplet aerosols generated by mouth coughing and nose breathing in an air-conditioned room[J]. Sustain Cities Soc, 2019, 51: 101721. DOI:10.1016/j.scs.2019.101721 |
| [12] |
张廷杰, 邹皓, 曾勇, 等. 曳引驱动乘客电梯的运行舒适度检测[J]. 中国测试, 2020, 46(9): 143-147. Zhang TJ, Zou H, Zeng Y, et al. Comfort detection of traction driven passenger elevator[J]. China Measurement & Test, 2020, 46(9): 143-147. |
| [13] |
Zhu SW, Kato S, Yang JH. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment[J]. Build Environ, 2006, 41(12): 1691-1702. DOI:10.1016/j.buildenv.2005.06.024 |
| [14] |
张毅. 置换通风温度分层对人际间飞沫传播的影响机理研究[D]. 西安: 西安建筑科技大学, 2019. Zhang Y. Study on the influence of temperature stratification in displacement ventilation on interpersonal droplet transmission[D]. Xi'an: Xi'an University of Architecture and Technology, 2019. |
| [15] |
孙一坚, 沈恒根. 工业通风[M]. 4版. 北京: 中国建筑工业出版社, 2010. Sun YJ, Shen HG. Industrial ventilation[M]. Fourth edition. Beijing: China Construction Industry Press, 2010. |
| [16] |
Ansys Inc (2018)[M]. ANSYS Help.
|
| [17] |
安朴艳. 室内气流组织及颗粒物分布的数值模拟研究[D]. 长沙: 湖南大学, 2016. An PY. Numerical simulation research of air and particles matter distribution in indoor room[D]. Changsha: Hunan University, 2016. |
| [18] |
蔡增基, 龙天渝. 流体力学泵与风机[M]. 5版. 北京: 中国建筑工业出版社, 2009. Cai ZJ, Long TY. Hydrodynamic pump and air fan[M]. Fifth edition. Beijing: China Construction Industry Press, 2009. |
| [19] |
郑聪. 人员密集场所室内流场实验及数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. Zheng C. Study on indoor flow field under the crowding conditions by experiments and numerical simulations[D]. Harbin: Harbin Institute of Technology, 2015. |
| [20] |
Duguid JP. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei[J]. J Hyg (Lond), 1946, 44(6): 471-479. |
| [21] |
刘鹏, 张华玲, 李丹. 人体飞沫室内传播的动力学特性[J]. 制冷与空调(四川), 2016, 30(4): 371-376. Liu P, Zhang HL, Li D. Dynamic characteristics of human droplet indoor transmission[J]. Refrigeration and Air Conditioning (Sichuan), 2016, 30(4): 371-376. DOI:10.3969/j.issn.1671-6612.2016.04.001 |
| [22] |
Yang CQ, Yang XD, Zhao B. Person to person droplets transmission characteristics in unidirectional ventilated protective isolation room: The impact of initial droplet size[J]. Build Simul, 2016, 9(5): 597-606. DOI:10.1007/s12273-016-0290-7 |
| [23] |
Zhang L, Li YG. Dispersion of coughed droplets in a fully-occupied high-speed rail cabin[J]. Build Environ, 2012, 47: 58-66. DOI:10.1016/j.buildenv.2011.03.015 |



